Ruixiang Li

Image Stitching图像拼接

Panorama全景

提取特征 -> 特征匹配 -> 解决变换 -> 混合图像

Solve Transformations变换

• Filtering滤波：改变图像的范围（值域） $g(x)=\textcolor{red}{T(}f(x)\textcolor{red}{)}$

• Warping扭曲：改变图像的区域Domain（定义域） $g(x)=f(\textcolor{red}{T(}x\textcolor{red}{)})$

T 对所有点都是相同的，并且不依赖于图像内容；p 和 p’ 是二维像素坐标。

（Translation、Rotation、Aspect、Affine、Perspective、Cylindrical）

1.齐次坐标(Homogeneous Coordinates)变换

齐次坐标：

\[(x,y)\Rightarrow\begin{bmatrix} x\\y\\1\end{bmatrix}, \begin{bmatrix} x\\y\\w\end{bmatrix}\Rightarrow(x/w,y/w)\]

线性变换加平移（有 6 个自由度）：

\[\begin{bmatrix} x'\\y'\\1\end{bmatrix}\equiv\begin{bmatrix} a&b&c\\d&e&f\\0&0&1\end{bmatrix}\begin{bmatrix} x\\y\\1\end{bmatrix} \equiv T\begin{bmatrix} x\\y\\1\end{bmatrix}\]

我们得到没有齐次坐标的以下变换：

\[x'=Ax+b\]

我们就可以做相应的变换：平移、拉伸、二维平面内旋转、剪切等

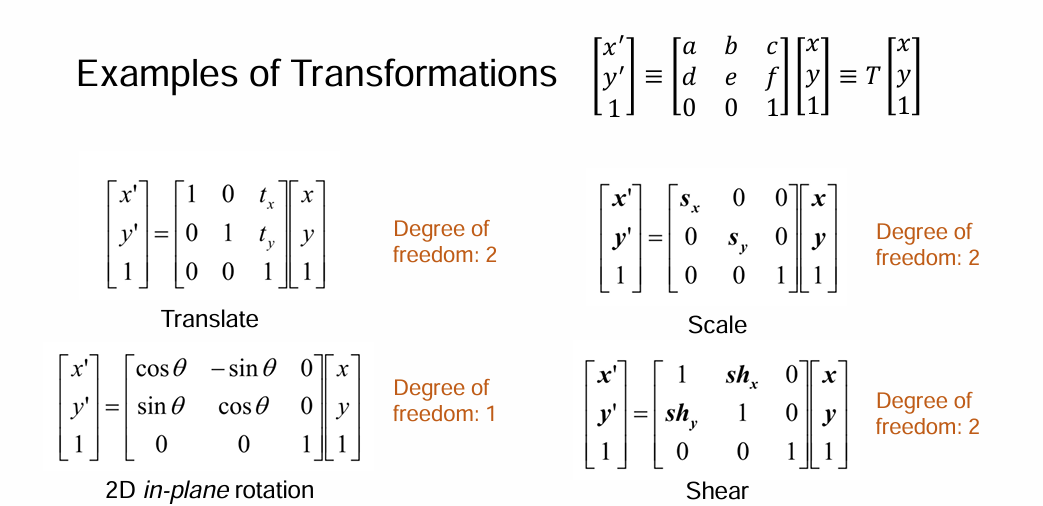
我们将前后两个图片上的对应点联立，可以有：

\[\begin{bmatrix} x_i' \\ y_i' \end{bmatrix} = \begin{bmatrix} a & b \\ d & e \end{bmatrix} \begin{bmatrix} x_i \\ y_i \end{bmatrix} + \begin{bmatrix} c \\ f \end{bmatrix}\]

我们考虑应该如何求解 abcdef 这六个变量？将上述方程转化为更大的稀疏矩阵：

\[\begin{bmatrix} x_i' \\ y_i' \\ \vdots \end{bmatrix} = \begin{bmatrix} x_i & y_i & 0 & 0 & 1 & 0 \\ 0 & 0 & x_i & y_i & 0 & 1 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \end{bmatrix} \begin{bmatrix} a \\ b \\ d \\ e \\ c \\ f \end{bmatrix}\]

即： $\mathbf{b}{2n \times 1} = \mathbf{A}{2n \times 6} \mathbf{t}_{6 \times 1}$ 。我们发现每一对对应点可以得到两个方程，那么只需要3个不共线的点就可以求解上述线性方程组。

但是在现实中，我们可以找到很多组点对，他们求解的结果可能会出现误差。于是我们考虑最小二乘法，通过最小化能量来求全局最优解：

\[E = \|A t - b\|_2^2 = t^T A^T A t - 2 t^T A^T b + b^T b\]

E 是一个二次函数，为了求解最小值（广义解），我们对其求导并令其导数为 0（显然$A^TA$是一个满秩矩阵）：

\[A^T A t = A^T b,t = (A^T A)^{-1} A^T b\]

但是进行图像拼接时，两张图片往往只有一部分可以对应，这不是一个仿射变换。所以我们将上述的$3\times3$矩阵$T$的最后一行替换为另外三个参数：$[g,h,i]$。就得到了：Homography单应矩阵。

2. 单应矩阵Homography

单应矩阵用来匹配两个并不完全重合的图片，将其投射在同一平面上，因此相对于齐次坐标变换矩阵，最后一行会进行修改：

\[\begin{bmatrix} a&b&c\\d&e&f\\g&h&i \end{bmatrix}\]

由于变换过程中没有信息损失，单应矩阵一定是满秩矩阵；

变换后的平面图像与原图像共享同一个相机中心；

由于该矩阵定义在齐次坐标下，乘以一个非0标量后，对其变换效果没有影响，所以其自由度为$9-1=8$，也就是需要重合部分的4个点才可以计算确定单应矩阵。

单应矩阵既可以用于同一平面上不同位置画面的变换，也可以用于来自两个共享相同中心的摄像机的图像之间的变换

求解：

设对应点：$[x_i,y_i]\leftrightarrow[x_i’,y_i’]$，有：

\[\begin{bmatrix} x'_i \\ y'_i \\ 1 \end{bmatrix} \cong \begin{bmatrix} h_{00} & h_{01} & h_{02} \\ h_{10} & h_{11} & h_{12} \\ h_{20} & h_{21} & h_{22} \end{bmatrix} \begin{bmatrix} x_i \\ y_i \\ 1 \end{bmatrix}\]

由于单应矩阵只有8个自由度，我们可以设$h_{22}=1$做归一化，也可以令$|[h_{00},h_{01},…,h_{22}]|_2=1$，总之对矩阵要进行额外的约束。

将矩阵乘法展开，得到：

\[x'_i (h_{20}x_i + h_{21}y_i + h_{22}) = h_{00}x_i + h_{01}y_i + h_{02} \\ y'_i (h_{20}x_i + h_{21}y_i + h_{22}) = h_{10}x_i + h_{11}y_i + h_{12}\]

在考虑多个对应点对后，可得齐次线性方程组$A_{2n\times 9}h_9=0_{2n}$：

\[\begin{bmatrix} x_1 & y_1 & 1 & 0 & 0 & 0 & -x'_1x_1 & -x'_1y_1 & -x'_1 \\ 0 & 0 & 0 & x_1 & y_1 & 1 & -y'_1x_1 & -y'_1y_1 & -y'_1 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ x_n & y_n & 1 & 0 & 0 & 0 & -x'_nx_n & -x'_ny_n & -x'_n \\ 0 & 0 & 0 & x_n & y_n & 1 & -y'_nx_n & -y'_ny_n & -y'_n \end{bmatrix} \begin{bmatrix} h_{00} \\ h_{01} \\ h_{02} \\ h_{10} \\ h_{11} \\ h_{12} \\ h_{20} \\ h_{21} \\ h_{22} \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ \vdots \\ 0 \end{bmatrix}\]

所以只需要4组不共线的对应点对 + 一个约束条件即可求解该方程组。

事实上，我们往往通过特征匹配，可以找到远超4个的点对。于是我们在$|h|^2=1$的条件下考虑能量函数$E$ 并使其最小化：

\[E = \|Ah\|^2 + \lambda \left(\|h\|^2 - 1\right) = h^T A^T A h + \lambda h^T h - \lambda\]

这里考虑的能量函数其实是在二次型的基础上引入拉格朗日乘子的约束条件。

拉格朗日乘子法（Lagrange multipliers）是一种寻找多元函数在一组约束下的极值的方法。

显然$E$是一个二次型，我们对其求导并令其导数为 0，得到：

\[\frac{\partial E}{\partial h}=2A^TAh+2\lambda h=0,A^TAh=-\lambda h, E=-\lambda\]

即$E$最小时，$-\lambda$也最小，$h$是矩阵$A^TA$这个对称矩阵最小特征值的特征向量。

注：$|Ah|^2$表述了代数误差，我们同样可以最小化几何误差来求解：

\[\sum_{i=1}^{k} \left\|[x'_i, y'_i] - T([x_i, y_i])\right\|^2 + \left\|[x_i, y_i] - T^{-1}([x'_i, y'_i])\right\|^2\]

Feature Matching特征匹配

首先考虑线性回归：

\[y=ax+b,E=\sum_i(ax_i+b-y_i)^2\]

离群值（Outlier） 指的是在数据集中偏离其他数据点的极端数据点，由于误差函数是平方项，其平方会放大对总误差的贡献。离群值通常偏离真实线性趋势较远，因此会占用大量权重，从而显著影响最终回归结果。

其实就是相当于二维线性回归过程中出现的过于偏离拟合直线的点。高中数学告诉我们应该剔除这些点再拟合，也是出于减少离群值影响的想法。

（否则就会出现某些论文里面的离谱数据拟合）

减少离群值的影响，是解决问题的核心途径。可以通过数据清理、选择更鲁棒的误差函数或采用鲁棒优化方法来降低离群值的干扰，从而获得更准确的回归模型。

于是便有了RANSAC：随机抽样一致算法

RANSAC：RANdom SAmple Consensus

RANSAC是一种经典的迭代式鲁棒拟合算法，常被用于解决离群点（Outliers）对模型拟合的干扰问题。其流程如下：

1. 随机取样。（通常取可以确定模型的最小样本点，例如二维线性回归只需要两个点，单应矩阵需要4个点）

2. 拟合模型，统计内点（Inliers）。（一般将误差在一定范围内的点均记为内点）

3. 迭代。（重复一定次数，通常是使用统计方法确定一个适合的迭代次数。）

4. 选择。（选择可以拟合最多内点的模型，抛弃其他离群点）

1. 如何找到内点？

通过设置内点容忍阈值（如几何误差），筛选误差较小的数据点作为内点。

2. 迭代何时终止？

迭代次数 N 的设置需要保证算法可靠性，通常遵循如下规律：

\[N>\frac{\log e}{\log(1-G^P)}\]

• 数据中离群点比例越高（G 越低），所需迭代次数越多。
• 拟合所需点数 P 增加，所需迭代次数也增加。

RANSAC的优点在于简单且同用，可以适用于多种问题且表现良好；缺点则是过于依赖超参数，一旦内点比例较低或问题复杂，就需要过多的迭代次数来保证拟合成功率。

就像ICS的核心内容：权衡。我们需要权衡迭代次数带来的拟合成功率与随之而来的计算开销（时间、内存、能量……）

Image Blending图像混合

怎么创建全景图Panorama？