Ruixiang Li
Image Processing图像处理
Image Processing图像处理
一张图片就是一个二维函数$I(x, y)\in[0,255]\in\mathbb{Z}$，$(x,y)\in([1,width],[1,height])$，有颜色图则是$I(x, y,c)$。（注：左上角为原点，上x左y。）
1.像素/点处理
| 处理 | 函数 |
|---|---|
| 原样 | $I(x,y)$ |
| 暗化darken | $I(x,y)-128$ |
| 亮化lighten | $I(x,y)+128$ |
| 低对比low contrast | $I(x,y)/2$ |
| 反相invert | $255-I(x,y)$ |
| 灰度图gray | $dot([0.3,0.6,0.1],I(x,y))$ |
我们可以将图像像素处理总结为：
\[g(x)=a(x)f(x)+b(x)\]其中$f(x)$是处理前的像素，$a(x)$调整像素的对比度，$b(x)$调整像素的明暗程度。
2.Histogram Equalization直方图均衡化
首先将原图像的直方图（纵轴数量，横轴亮度/像素值）绘制出来，可以发现不同位置颜色和亮度分布非常不均匀。
首先我们计算像素（在不同亮度下）的累积分布，除以总数后得到概率密度的累积分布图；再映射到[0, 255]，就得到了原图像像素值到新像素值的映射，也就实现了直方图均衡化。
直方图均衡化通过对图像的亮度值进行转化，使像素值按更均匀的分布排列，凸显更多的细节。（其实就是按排名分布像素值）
- 数学原理？随机数生成(Random Number Generator)！
先考虑一个均匀分布(Uniform distribution) 的随机数生成器$U$：
\[U_n=(aU_{n-1}+c)\mod{m}\]这是一个线性同余生成器，$a$、$c$、$m$均为质数，用于生成伪随机数。为了让生成的随机变量$X$能够服从某种分布，我们需要$X$的累积分布函数CDF：$F(X)$，则有：
\[X=F^{-1}(U)\]将均匀分布$U$转化为随机变量$X$。
- 证明：
直方图均衡化也使用了类似的逆变换原理。它将原始图像的灰度值当作随机变量，通过其累积分布函数（CDF）对其进行均衡化，使得输出灰度值更加均匀。
这种方法可以实现任意两种发布的互相转化。
Image Filter图像滤波（线性）
像素/点操作可以看作 1x1 的滤波。
-
图像$I(i,j)$：$w\times h$的数字图像；
-
$h(u,v)$：$m\times n$的滤波器(filter) or 滤波核\卷积核(Kernel)
-
假设m、n均为奇数，p、q为m/2和n/2向下取整；
输出像素可以视为输入像素一个邻域内像素的加权平均。
然后处理边界？
-
忽略？会造成图像大小缩减；
-
补零？没有图像的地方全为0；
-
假设图像周期分布？左侧没有右侧补；
-
反射？最大h，h+1=h-1；
torch.nn.functional.pad(image, pad, mode="contant", value = None).
mode - 'constant', 'reflect' or 'circular'
（一般要求Kernel总和为1，以免导致图像亮度变化）
1.Box Fliter
\[\frac{1}{9}\begin{bmatrix} 1&1&1\\1&1&1\\1&1&1 \end{bmatrix}\]模糊图像。
2.Gaussian Filter/Low Pass Filtering高斯滤波/低通滤波
指定$\sigma^2 =1$：
\[\frac{1}{16}\begin{bmatrix} 1&2&1\\2&4&2\\1&2&1 \end{bmatrix}\]模糊图像，但过渡平滑，更加自然，能够更好地保留边缘和降噪。
3.Sharpening Filter锐化滤波
\[\begin{bmatrix} 0&0&0\\0&2&0\\0&0&0 \end{bmatrix}-\frac{1}{9}\begin{bmatrix} 1&1&1\\1&1&1\\1&1&1 \end{bmatrix}\\ I+\lambda (I-I_{blur})\]可以提高图像对比度，即“锐化”：突出高频去低频
为了加速滤波，有一些滤波器是 “可分离的”(Separable)：
Separable Filtering
我们可以将一个二维的滤波器分解为两个一维滤波器，将每个像素的运算次数从$K^2$降到$2K$，其中：$K=vh^T$：
\[\frac{1}{K^2}\begin{bmatrix} 1&1&\cdots&1\\1&1&\cdots&1\\\vdots&\vdots&\ddots&\vdots\\1&1&\dots&1 \end{bmatrix}\rightarrow \frac{1}{K}[1,1,\cdots,1]\] \[\frac{1}{16}\begin{bmatrix} 1&2&1\\2&4&2\\1&2&1 \end{bmatrix}\rightarrow \frac{1}{4}[1,2,1]\]Properties
数学中称为Cross-Correlation：
\[g(i, j) = \sum_{k, l} f(i + k, j + l) h(k, l)\]而卷积Convolution：
\[g(i, j) = \sum_{k, l} f(i - k, j - l) h(k, l) \\= \sum_{k, l} f(k, l) h(i - k, j - l)\]相较于“相关”，卷积还需要对卷积核进行翻转。
对于卷积神经网络，其实是在作“相关”运算。两者都称为 “线性移位不变性linear shift-invariant”LSI 运算：
-
Linear：$h \circ (f_0 + f_1) = h \circ f_0 + h \circ f_1$
-
Shift-invariant等变性：$g(i, j) = f(i + k, j + l) \iff (h \circ g)(i, j) = (h \circ f)(i + k, j + l)$
卷积操作是CNN的核心，网络通过卷积层提取特征。
输入数据 > 卷积层 > ReLU激活 > 池化 > 全连接层 > 分类
卷积和相关两者都可以表示为矩阵向量的乘积：
\[g=Hf\]即使用一个稀疏矩阵来进行相关操作，例如：
\[[72,88,62,52,37]\cdot[\frac{1}{4},\frac{1}{2},\frac{1}{4}]\rightarrow \frac{1}{4}\begin{bmatrix} 2 & 1 & & & \\ 1 & 2 & 1 & & \\ & 1 & 2 & 1 & \\ & & 1 & 2 & 1 \\ & & & 1 & 2 \end{bmatrix} \begin{bmatrix}72\\88\\62\\52\\37\end{bmatrix}\]Non-Linear Filter（非线性滤波）
1.Median Filter中值滤波
高斯滤波的问题#1：不能很好地去除噪音、且边缘模糊。
中值滤波器：对于给定范围内，取到中间值的滤波器。
可以有效减少某些类型的噪音，如脉冲噪音（也称为‘椒盐’噪音或‘瞬态’噪音）。中值滤波使得具有不同值的点更像它们的邻居。
2.Bilateral Filter双边滤波
高斯滤波的问题#2：滤波核在整个图像中是均匀的。它不依赖于图像的内容。
双边滤波/Content-Aware Dynamic Filter内容感知动态过滤器：滤波核与图像内容有关，既可以去除噪音，又可以很好得保留特征。实现双边滤波器需要两个高斯：
- Domain Kernel：以距离为特征的高斯核，反映像素与中心偏离程度与权重的关系。
- Range Kernel：以图像差异为特征的高斯核，反映像素与中心像素值差异与权重关系。像素/颜色差异越大，权重越小。
- Bilateral Filter：domain * range，双边滤波器
最后在滤波过程中对结果作归一化：
\[\mathbf{g}(i, j) = \frac{\sum_{k, l} \mathbf{f}(k, l) w(i, j, k, l)}{\sum_{k, l} w(i, j, k, l)}\]对一张图片连续使用5次双边滤波后会有卡通风格（临近像素同化为几乎同种颜色，差异较大的像素块之间差异增大，形成类似油画分块上色的卡通效果）
Attention？(*)
对于归一化过程，我们可以认为这是一个softmax函数：
\[BilateralFilter=softmax(-(F_i-F_j)^2/\sigma)\]我们可以调整filter为具有动态权重的Attention（Attention机制本身就会考虑不同方面的相关性，可以视为广义的Filter）
\[Attention(X_q,X_k,X_v)=softmax(\frac{QK^T}{\sqrt{D}})V\]Application of Filters应用
1.Template Matching模板匹配
模板匹配最经典的引发是人脸识别，将其转化为一个Template在图像种找最高相似性的问题。
我们将这个Template作为一个Kernel对图像作滤波，亮度最高的位置就是目标位置。
\[g(i, j) = \sum_{k, l} f(i + k, j + l) h(k, l)\]为了防止局部像素太大导致错判，我们对结果做一次归一化；
\[g(i, j) = \frac{\sum_{k, l} f(i + k, j + l) h(k, l)}{\sqrt{\sum_{k, l} f(i + k, j + l)^2} \sqrt{\sum_{k, l} h(k, l)^2}}\]2.Photography with Flash/No-Flash Pair
在昏暗条件下拍摄存在的问题：
-
开闪光灯：明亮、清晰、噪音小，但失去原本光源的信息
-
无闪光灯：保留原光源、更加自然、有氛围，但光线昏暗、缺失细节、噪音大。
能不能将两张图片的优点结合？有的，兄弟有的。下称两张图片为No-Flash和Flash。
对No-Flash作双边滤波时，如果$\sigma_r$太大会造成过度平滑；太小则会导致平滑效果差，不能很好地去噪。但我们不能直接拿带噪音的图像去衡量相似性，调整到不大不小可以，但并不perfect。于是，我们可以想到：拿Flash这张无噪声的图片来衡量相似性。
所以我们引入Joint Bilateral Filter联合双边滤波：
加入另一张图像作为引导图，告诉他哪两个像素很相像：对No-Flash作用Domain Kernel、而对Flash使用Range Kernel，即距离权重保持不变，但颜色权重使用引导图权重。
（类似Attention中的Cross-Attention）
接下来还需要处理怎么加入细节的问题：因为现在有Flash这个无噪点且有细节的图片，我们对Flash做一次双边滤波，将原图像各点与滤波后图像作除法，得到具有细节信息的图像(Detail Layer)。
（不用减法是因为两个图像色调不一样。提取图像细节的本质是保留甚至扩大对比度对比度信息）
最后将提取到的特征乘到联合双边滤波后的图像上，就可以即保留色调又保留细节。
Upsampling/Downsampling Pyramids
上采样/下采样：宏观上可以理解为在保证图像可视（即没有噪点、锯齿等因素）的条件下放大缩小图像（即改变分辨率）。
Subsampling（其实就是Downsampling）
当采样率不足时，会出现 “走样”Aliasing，导致图像细节缺失。为了解决走样问题，我们首先需要将图像的高频消息滤除。而高斯滤波就可以平滑高频信息。（又称低通滤波）
在信号处理领域（包括图像处理），频率表示信号变化的速率：
- 低频信息： 信号变化缓慢，例如大面积的均匀颜色、渐变的区域。代表图像的整体结构或全局信息。
- 高频信息： 信号变化快，例如图像中的边缘轮廓、复杂的纹理、噪声等。高频信息决定了图像的细节。
Gaussian Pyramid高斯金字塔
从原图像出发，每进行一次模糊（高斯滤波）+ 一次下采样，即得金字塔的下一层。
example：Detection人脸检测
例如，对于一个M x M的人脸模板，需要在N x N的图片上匹配，将模板逐步放大后进行滤波比较的计算开销太大，于是可以将图像做高斯金字塔，并以此进行模板匹配。
Upsampling升采样
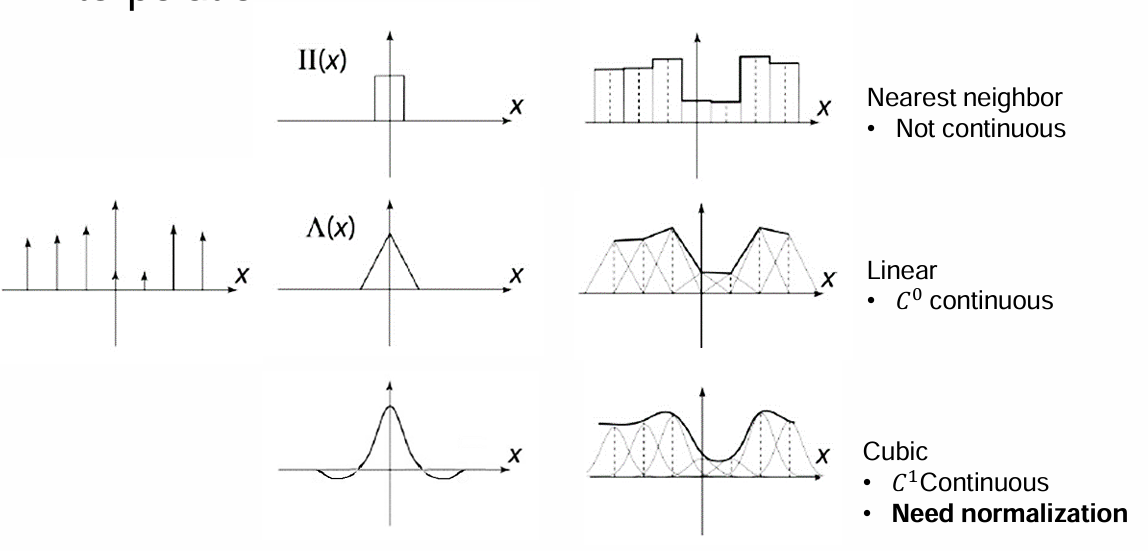
升采样最简单的想法是 “Nearest neighbor interpolation”最近邻插值，即直接将最近的像素复制过去。但是这样得到的结果并不平滑。
Interpotion插值：
插值是一种基于一组已知离散数据点来构造（或寻找）新的数据点的方法。
\[g(x)=\sum_kc_ku(\frac{x-x_k}{h})\]
- $g$：插值函数
- $h$：采样增量
- $x_k$：插值节点
- $c_k$：基于采样数据计算得到的参数
- $u$：插值核（interpotion kernel） $u(0)=1$，否则$u(k)=1$
例如使用box filter作为$u$，就可以对应到最近邻插值。但是得到的结果并不连续；
改进后我们可以使用线性插值作为$u$，得到的函数是$C^0$连续的。但是在原函数采样点处仍然不连续；
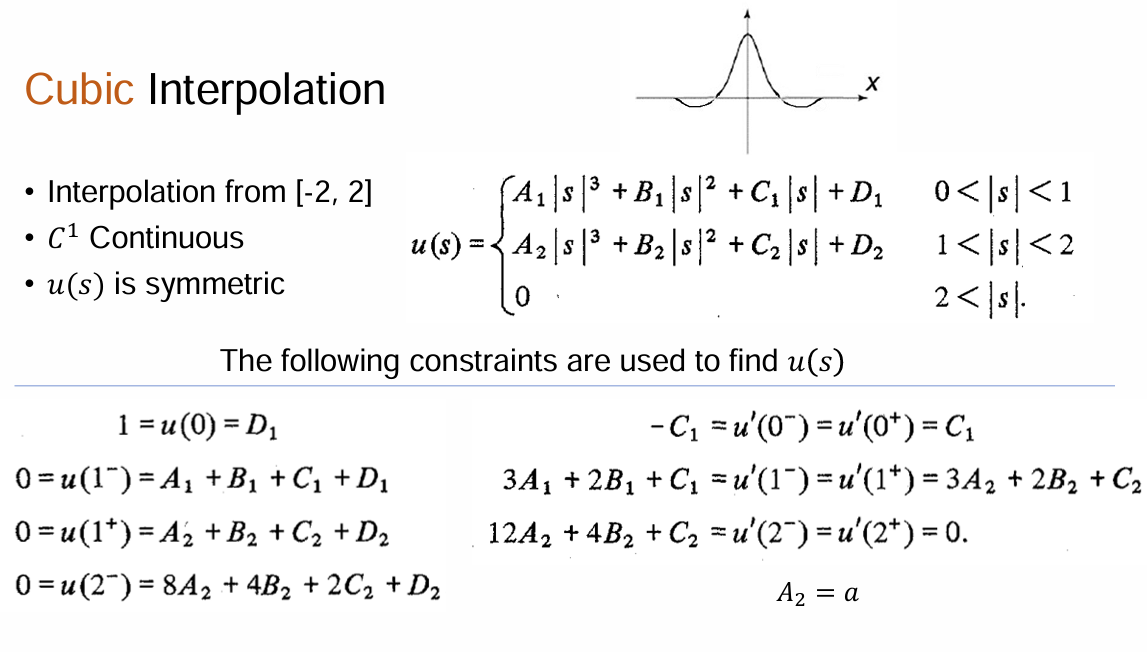
继续改进后就得到了Cubic插值，得到的函数是$C^1$连续的。其插值范围是$[-2,2]$，具体推导（反正就是待定系数法）见下：
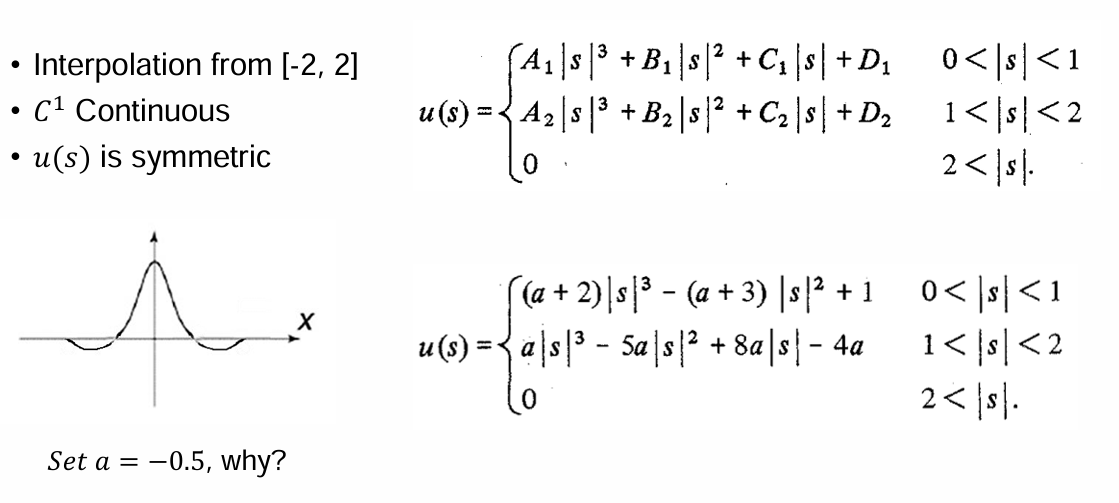
对于图像插值，就是在某个方向上插值，将得到的结果在另一个方向上再次插值。所以，图像插值需要附近的4个点。
而像素对齐的方式，也会极大的影响插值效果。使用pytorch进行图像处理时，可以选择角点对齐的形式，如下：
近似(Approximation) 和 插值(Interpotion) 的区别在于，插值对于所需的函数有一定要求。他要求函数在目标点处为1，其他地方为0；但近似并不要求结果函数结果采样点，例如：
\[g(x) = \frac{\sum_k c_k u\left(\frac{x - x_k}{h}\right)}{\sum_k u\left(\frac{x - x_k}{h}\right)} ,u(x) > 0\]