Ruixiang Li

Lecture12：Cache Memories

Cache memoty organization and operation

Cache缓存是小型的、由高速SRAM实现的存储结构，完全由硬件管理。其包含在CPU内，处于“寄存器组”附近的缓存的实质是存储有主存储器中经常访问的块。出于“局部性”原则，大多数请求会由Cache提供，仅花费几个时钟周期。

1.General Cache Organization-S,E,B

由于缓存完全由硬件管理，硬件需要知道如何查找有关块，并且知道是否为所需的块。所以必须用严格且简单的方式组织Cache。

关于查找逻辑，Cache由lines和sets组成。Cache由S=2^s个set组成，每个set由E=2^e个line组成，而每个line由B=2^b个字节的数据块data、一个vaild bit（指示数据位和数据块存在）以及一个tag标记位（帮助搜寻）组成。

Cache Size = S * E * B（组、行、块）

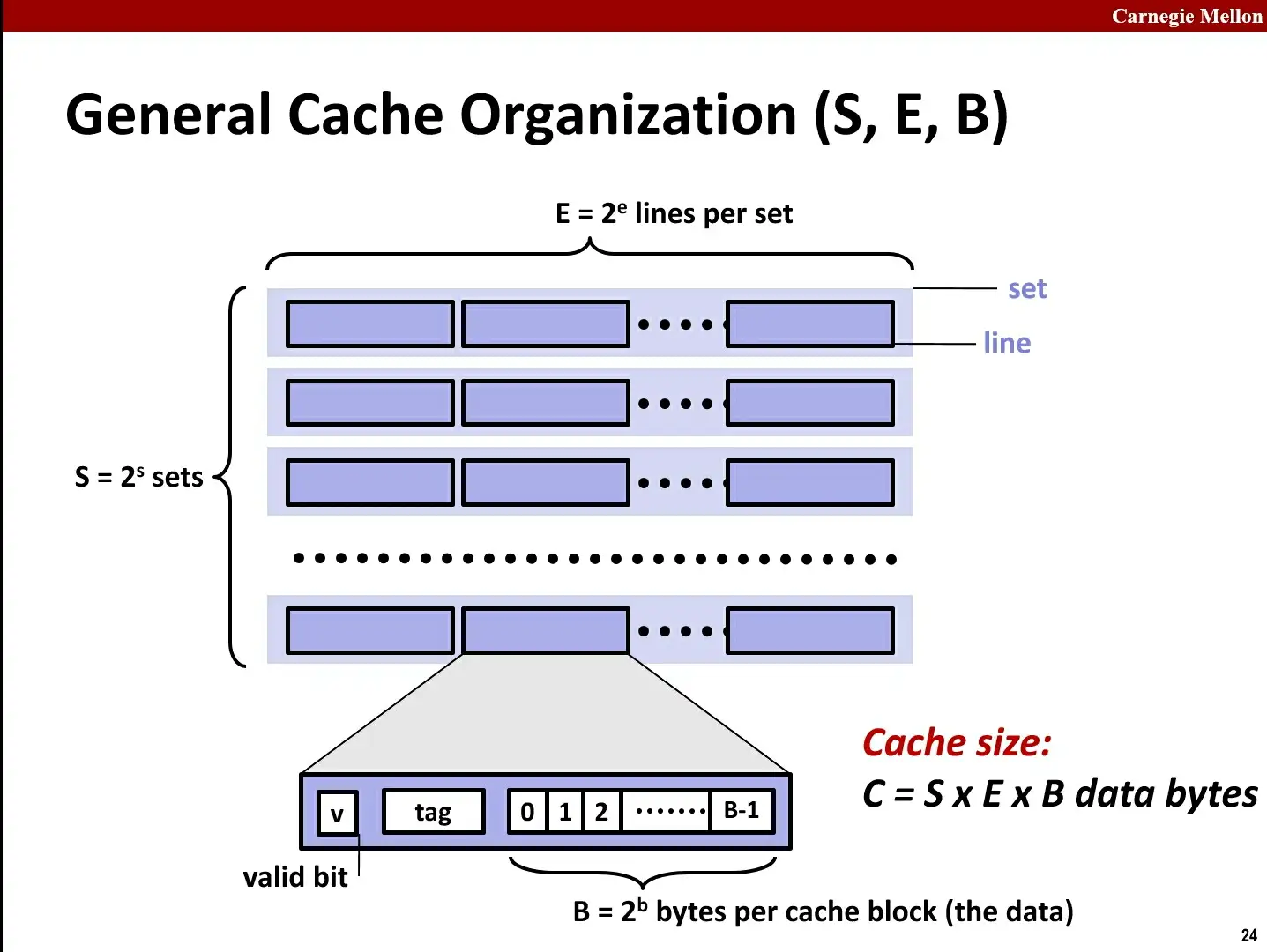
2.Cache Read

Address of Word：（在x86-64上为64位）

t bits	s bits	b bits
tag	set index	block offset

tag：代表标记位，用来区分不同的缓存块。负责缓存块的匹配与验证。
set index：代表组索引，用于确定在缓存中应该存储在哪一组。帮助定位具体分配的组。
block offset：代表块偏移，用于定位缓存块中的具体字节。在组内定位具体的字节。

从缓存读取数据时，首先确定组，然后逐一检查组内的行/缓存块（对比Tag部分和检查valid bit ?= 1），确定数据是否命中（hit），然后根据块偏移定位准确位置。

example#1

E = 1，即Direct Mapped Cache直接映射缓存（每个set只有一个line）

address of int：t bits + 0…01 + 100

则组索引为1，块偏移为4（偏移从0开始），并且在读取4 Bytes（int）后返回CPU并存入寄存器。

如果未命中，则旧line会被清除后从主存中读取的新数据覆盖，之后再读取、返回。

example#2

E = 2（E > 1，即E-way Set Associative Cache E路相连高速缓存 or 组相连高速缓存），每个set中有2个line，每个block中有 8 bytes。

address of short int：t bits + 0…01 + 100

当查找到对应的set组后，Cache会并行查找所有的line，比较tag和valid。如果有匹配的line则缓存命中，否则缓存未命中。

对于未命中后需要被替换的块，最常用的算法是 “最近最少使用”策略。即将长时间不被引用（根据局部性，将来也不太可能被引用）的块替换。当替换组中的一个行时，如果数据已经更改，必须将其写回内存。

Inter系统的L3缓存是16组相联，其他大多为8路。

example#3

如果我们要求电路非常便宜，那么只能存在一个组S = 1，称为Fully Associative Cache全相联高速缓存。

不用hash来确定组，直接挨个比对高位地址，来确定是否命中。可以想见这种方式不适合大的缓存。

如果4M 的大缓存，linesize为32Byte，采用全相联的话，就意味着4 * 1024 * 1024 / 32 = 128K 个line挨个比较，来确定是否命中，这是多要命的事情。高速缓存立马成了低速缓存了。

所以，比较复杂的搜索算法和硬件实现是有值得的。特别是在虚拟存储中，DRAM实现的完全关联的高速缓存，来自硬盘的块可以存储在任何地方。

3.Writes？

数据存在多份副本：L1、L2、L3、主存、硬盘

white-hit：

Write-Through：直接将块写入memory，内存始终保存缓存的镜像。expensive！
Write-Back：直到我们需要替换/覆盖这个块的时候再写回内存，只是推迟了写入时间。写回操作需要额外的位（在line中）表示是否已经写入了这些块。

white-miss：

就是写入的字并不在缓存中。

Write-allocate：先将数据从主存（Main Memory）加载到缓存中，然后再执行写操作。（与Write-Back配合，且更常用）
No-write-allocate：并不将写入位置读入缓存，直接把要写的数据写入到内存中。这种方式下，只有读操作会被缓存。（与Write-through配合）

在Inter Core i7的缓存结构中：

缓存	大小	E=?	Access/cycles 访问/时钟周期	作用
L1 i-cache/d-cache	32KB	8	4	指令缓存/数据缓存，直接与寄存器交互
L2 unified cache	256KB	8	10	连接L1和L3
L3 unified cache	8MB	16	40-75	被所有核共享，连接主存和L2

4.Cache Performance Metrics

未命中率 (Miss Rate)：未在缓存中找到的内存引用占总内存访问的比例（未命中 / 访问次数）。未命中率=1−命中率典型值（百分比）：L1 缓存3%-10%，L2 缓存：可能非常小（例如，<1%，具体取决于缓存大小等因素）。
命中时间 (Hit Time)

将缓存中的一行数据传递到处理器所需的时间，包括检查该数据是否在缓存中的时间。
- L1 缓存：4 个时钟周期
- L2 缓存：10 个时钟周期
未命中代价 (Miss Penalty)
- 因未命中而需要额外的时间。
- 对主存来说通常需要 50-200 个时钟周期（趋势：正在增加！）。

命中和未命中之间的差距是极大的，L1和主存之间的代价相差百倍。事实上，99%的命中率比97%的命中率好一倍（平均时间是一半）。

因此我们也需要编写缓存友好的代码，即具有更高的命中率，让常用部分更多。例如：重复引用、步长为1引用、

Performance impact of caches

1.The memory mountain

Read throughput(read bandwidth)吞吐量/带宽：

每秒从内存中读取的字节数 MB/s。

Memory mountain存储器山：根据空间局部性和时间局部性测量读取吞吐量。是一种紧凑的方法，用于表征内存系统性能。其将该存储系统的性能在该范围内作为二维函数绘制出来。（参考课本封面）

aaa

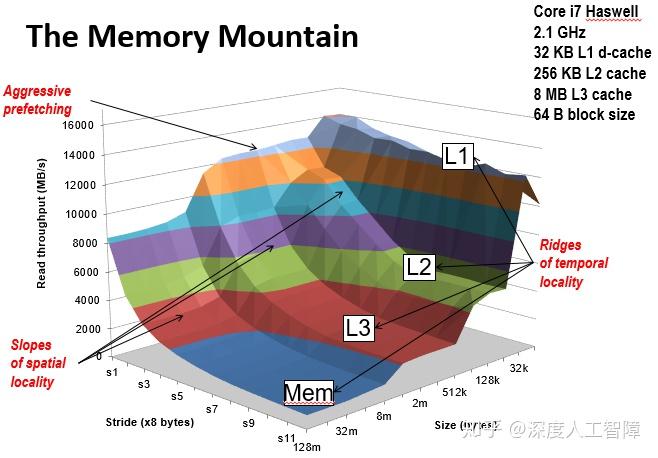
其中：

z轴表示吞吐量，单位：MB/s；
stride轴表示步长，单位：x8字节；
size轴是每次传递时要读取的元素总数量（工作集），单位：字节；

步长的增加会减少空间局部性，而size的增加会导致可以容纳数据的缓存更少。

固定步长时，读吞吐量随着工作集的增大呈阶梯状降低。出现的四级阶梯即为：L1、L2、L3、主存；
固定工作集大小时，空间局部性下降，读吞吐量随着步长的增大而平缓下降；
工作集越小，固定时间内访问工作集的次数越多，就越能体现出时间局部性，且总是在达到块尺寸大小时变平；
注意到步长为1时，读吞吐量随工作集大小变化非常缓慢。这是因为Core i7存储器系统中的硬件预取机制。这是一项很聪明的机制，也是对于撰写具有良好局部性程序的程序员的一种奖赏。
观察山上标有L2标记的山脊，可以发现：当步长很大时，读吞吐量不再下降。这是因为此时的步长已经超过了L2的大小，每次内存访问都不会命中。此时读吞吐量与步长没有关系，只由L3、L2之间高速缓存块的传送速度决定。

（注：上述分析来自知乎）

2.Rearranging loops to improve spatial locality

重排循环：以 N x N 矩阵乘法为例（改善空间局部性）

/* ijk */
for(i = 0; i < n; i++){
    for(j = 0; j < n; j++){
        cum = 0.0;
        for(k = 0; k < n; k++){
            sum += a[i][k] * b[k][j];
        }
        c[i][j] = sum;
    }
}

这段代码的时间复杂度为 O(n^3)。实际上，矩阵乘法不一定是这个顺序，可以证明改变循环顺序的另外5种排列依然可行。

对于ijk的顺序，在内循环中，矩阵A为行优先访问、矩阵B为列优先访问，在这种情况下，对于每次内循环的未命中次数，A每次会有0.25次未命中，而B有1次（每次都不会命中）（同jik）

而kij的顺序下，内循环的B、C都是行优先，平均每4次会出现一次未命中。（同ikj）

/* kij */
for(k = 0; k < n; k++){
    for(i = 0; i < n; i++){
    r = a[i][k]
    for(j = 0; j < n; j++)
        c[i][j] += r * b[k][j];
    }
}

jki的顺序下，内循环的A、C均为列优先：（同kji）

/* jki */
for(j = 0; j < n; j++){
    for(k = 0; k < n; k++){
        r = b[k][j];
        for(i = 0; i < n; i++)
            c[i][j] += a[i][k] * r;
    }
}

平均之下后，kij/ikj有着0.5次未命中，而最坏的jki/kji有2次未命中。（另外两种情况是1.25次）

3.Using blocking to improve temporal locality

Blocking阻塞：还是矩阵乘法（改善时间局部性）

c = (double *) calloc(sizeof(double), n*n);

/* Multiply n x n matrices a and b */
void mmm(double *a, double *b, double *c, int n) {
    int i, j, k;
    for (i = 0; i < n; i++)
        for (j = 0; j < n; j++)
            for (k = 0; k < n; k++)
                c[i*n + j] += a[i*n + k] * b[k*n + j];
}

假设矩阵元素为double，缓存大小为8 doubles，缓存大小远小于n。

对于这个没有阻塞的函数，第一次迭代下有n/8 + n = 9n/8次未命中，之后的迭代同理，总的未命中数为9n/8 * n^2 = (9/8) * n^3。（太大了）

加入阻塞后，有如下代码：

c = (double *) calloc(sizeof(double), n*n);

/* Multiply n x n matrices a and b */
void mmm(double *a, double *b, double *c, int n) {
    int i, j, k;
    for (i = 0; i < n; i+=B)
        for (j = 0; j < n; j+=B)
            for (k = 0; k < n; k+=B)
                /* B x B mini matrix multiplications */
                for (i1 = i; i1 < i+B; i1++)
                    for (j1 = j; j1 < j+B; j1++)
                        for (k1 = k; k1 < k+B; k1++)
                            c[i1*n+j1] += a[i1*n+k1] * b[k1*n+j1];
}

即将大矩阵分隔为更小的子矩阵后分别相乘。（线性代数告诉我们，分块矩阵乘法与原矩阵乘法等效）B = 1时即为原算法，其中保证了3B^2 < C。

这样总的未命中数为：n^3 / (4B)！